Random Numbers in C
Suppose we would like to simulate random die rolls. The C standard library
provides rand(), which returns pseudo-random integers from zero through
RAND_MAX, an arbitrary constant. One might be tempted to write
/* Returns a random integer in [1, 6] */
int rand_die(void)
{
/* Do not do this */
return 1 + rand() % 6;
}
This implementation does produce random integers from one through six, but it
neglects their distribution. Unless RAND_MAX + 1 happens to equal a multiple
of six, smaller outputs will occur with higher probability. To see how,
consider the case of RAND_MAX = 14:
rand() |
1 + rand() % 6 |
Probability |
|---|---|---|
| 0, 6, 12 | 1 | 3/15 |
| 1, 7, 13 | 2 | 3/15 |
| 2, 8, 14 | 3 | 3/15 |
| 3, 9 | 4 | 2/15 |
| 4, 10 | 5 | 2/15 |
| 5, 11 | 6 | 2/15 |
Because the possible values of rand() do not divide evenly across the die
faces, some outcomes occur with probability 3/15, while others occur with
probability 2/15. To fix this, we need to be more careful with our mapping:
/* Returns a uniformly distributed random integer in [0, n) */
int rand_below(int n)
{
assert(n > 0);
assert(n <= RAND_MAX);
int bin_width = RAND_MAX / n;
int limit = n * bin_width;
int r;
do {
r = rand();
} while (r >= limit);
return r / bin_width;
}
/* Returns a random integer in [1, 6] */
int rand_die(void)
{
return 1 + rand_below(6);
}
This solution divides the range of rand() into equally-sized bins, with each
bin corresponding to a possible output. If rand() returns a value outside
of the valid bins, it is simply called again.
rand() |
Result |
|---|---|
| 0, 1 | 1 |
| 2, 3 | 2 |
| 4, 5 | 3 |
| 6, 7 | 4 |
| 8, 9 | 5 |
| 10, 11 | 6 |
| 12, 13, 14 | retry |
Now, since each bin is the same width, the outcomes will occur with equal probability.
Does it matter?
I made a plot of the high and low probability error when rand() % N is used
to generate random numbers from zero through N - 1. Here we assume RAND_MAX
equals 32767, the smallest value allowed by the C standard.
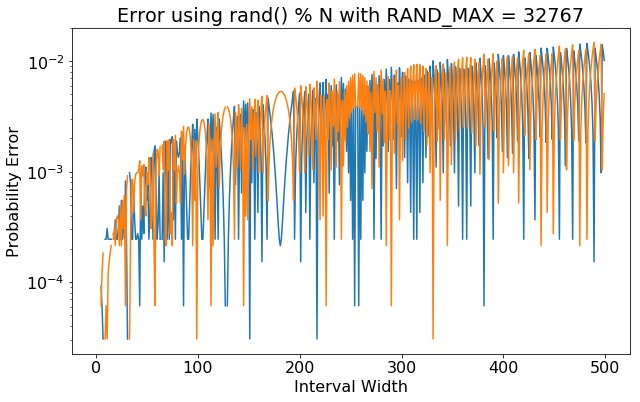
The relative error increases as the output interval grows. By N = 500
outcomes start to occur with probability 1% higher or lower than expected.